Hofstede's Long-term Orientation and Individuality: Obesity Relationships (using R)
Hofstede extended his original four dimensions, adding measures Long-Term Orientation (LTO) and Indulgence (Ind) in response to other researchers studies. While reading Hofstede's Cultures and Organizations: Software of the Mind, Third Edition I was struck by the lackluster reporting of the correlation between obesity and indulgence. It seemed obvious one would delve a bit further, maybe looking at a compound relationship between both indulgence and LTO, e.g., does short-sightedness and indulgence lead to obesity. Although I limit my analysis to OECD countries, that is what I present here.
An explanation of dimensions can be found on Hofstede's site.
Hofstede's Dimensions and Obesity
A first step would be to see what relationships exist between obesity and the dimensions:
Results - Regression and ANOVA
Both linear multiple regression and ANOVA would indicate that both individuality and LTO have, or at least one has, a relationship to obesity.
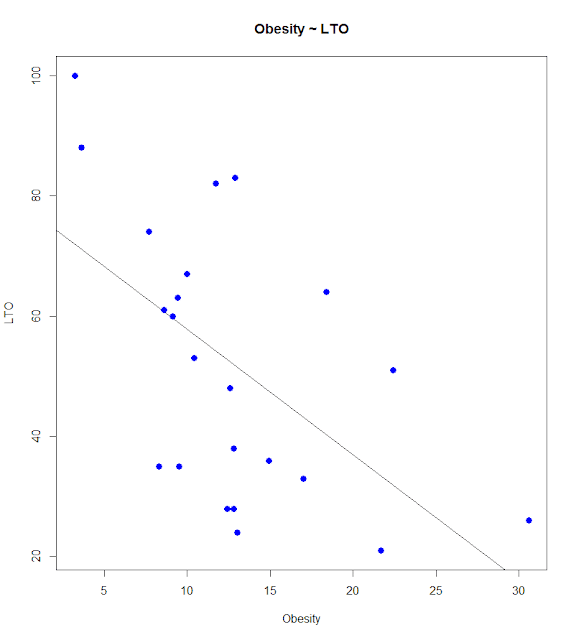
Correlations and Graphs - LTO and Obesity
The results seem significant, with a correlation of -.56.
Correlations and Graphs - Individuality and Obesity
These results seem equally significant, with a correlation of .59.
Concern - Correlation between Individuality and LTO
Although the two qualities are not linearly related, they have a significant degree of correlation, -.33.
Sample Data
An explanation of dimensions can be found on Hofstede's site.
Hofstede's Dimensions and Obesity
A first step would be to see what relationships exist between obesity and the dimensions:
1: # LM - Multiple Regression - New Hofstede, LTO and Ind
2: # Load the data into a matrix
3: rm(list = ls())
4: setwd("../Data")
5: oecdData <- read.table("OECD - Quality of Life.csv", header = TRUE, sep = ",")
6: print(names(oecdData))
7:
8: # Access the vectors
9: v1 <- oecdData$IQ
10: v2 <- oecdData$HofstederPowerDx
11: v3 <- oecdData$HofstederMasculinity
12: v4 <- oecdData$HofstederIndividuality
13: v5 <- oecdData$HofstederUncertaintyAvoidance
14: v6 <- oecdData$HofstederLongtermOrientation
15: v7 <- oecdData$HofstederIndulgence
16:
17: v9 <- oecdData$Gini
18: v10 <- oecdData$Obesity
19: v26 <- oecdData$Assaultsandthreats
20:
21: # Conclusion, both high individuality and low LTO contribute to obesity
22: # but inversely correlated with each other
23: # Obesity ~ Hofstede
24: relation1 <- lm(v10 ~ v2 + v3 + v4 + v5 + v6 + v7)
25: print(relation1)
26: print(summary(relation1))
27: print(anova(relation1))
Results - Regression and ANOVA
Both linear multiple regression and ANOVA would indicate that both individuality and LTO have, or at least one has, a relationship to obesity.
1: Call:
2: lm(formula = v10 ~ v2 + v3 + v4 + v5 + v6 + v7)
3:
4: Coefficients:
5: (Intercept) v2 v3 v4 v5 v6 v7
6: 1.09265 0.12813 0.07237 0.10560 -0.01969 -0.14108 0.08111
7:
8: Call:
9: lm(formula = v10 ~ v2 + v3 + v4 + v5 + v6 + v7)
10:
11: Residuals:
12: Min 1Q Median 3Q Max
13: -5.3248 -3.1639 -0.1943 1.3526 9.3436
14:
15: Coefficients:
16: Estimate Std. Error t value Pr(>|t|)
17: (Intercept) 1.09265 11.38472 0.096 0.9247
18: v2 0.12813 0.12105 1.059 0.3055
19: v3 0.07237 0.04969 1.456 0.1646
20: v4 0.10560 0.09187 1.150 0.2672
21: v5 -0.01969 0.10441 -0.189 0.8528
22: v6 -0.14108 0.05303 -2.660 0.0171 *
23: v7 0.08111 0.12755 0.636 0.5338
24:
25: Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
26:
27: Residual standard error: 4.715 on 16 degrees of freedom
28: (1 observation deleted due to missingness)
29: Multiple R-squared: 0.5731, Adjusted R-squared: 0.4131
30: F-statistic: 3.581 on 6 and 16 DF, p-value: 0.01919
31:
32: Analysis of Variance Table
33:
34: Response: v10
35: Df Sum Sq Mean Sq F value Pr(>F)
36: v2 1 26.81 26.814 1.2059 0.288389
37: v3 1 17.73 17.731 0.7974 0.385093
38: v4 1 253.50 253.495 11.4008 0.003846 **
39: v5 1 5.22 5.217 0.2346 0.634672
40: v6 1 165.43 165.431 7.4402 0.014902 *
41: v7 1 8.99 8.990 0.4043 0.533847
42: Residuals 16 355.76 22.235
43:
44: Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Correlations and Graphs - LTO and Obesity
1: # Corr - Obesity ~ LTO
2: cor.test(v6, v10)
3: plot(v10, v6, col = "blue", main = "Obesity ~ LTO", abline(lm(v6 ~ v10)), cex = 1.3, pch = 16, xlab = "Obesity", ylab = "LTO")
The results seem significant, with a correlation of -.56.
1: Pearson's product-moment correlation
2:
3: data: v6 and v10
4: t = -3.1025, df = 21, p-value = 0.005392
5: alternative hypothesis: true correlation is not equal to 0
6: 95 percent confidence interval:
7: -0.7902136 -0.1930253
8: sample estimates:
9: cor
10: -0.5606214
Correlations and Graphs - Individuality and Obesity
1: # Corr - Obesity ~ Idv
2: cor.test(v4, v10)
3: plot(v10, v4, col = "blue", main = "Obesity ~ Idv", abline(lm(v4 ~ v10)), cex = 1.3, pch = 16, xlab = "Obesity", ylab = "Idv")
These results seem equally significant, with a correlation of .59.
1: Pearson's product-moment correlation
2:
3: data: v4 and v10
4: t = 3.351, df = 21, p-value = 0.003027
5: alternative hypothesis: true correlation is not equal to 0
6: 95 percent confidence interval:
7: 0.2353225 0.8062918
8: sample estimates:
9: cor
10: 0.5902683
Concern - Correlation between Individuality and LTO
Although the two qualities are not linearly related, they have a significant degree of correlation, -.33.
Sample Data



Comments
Post a Comment